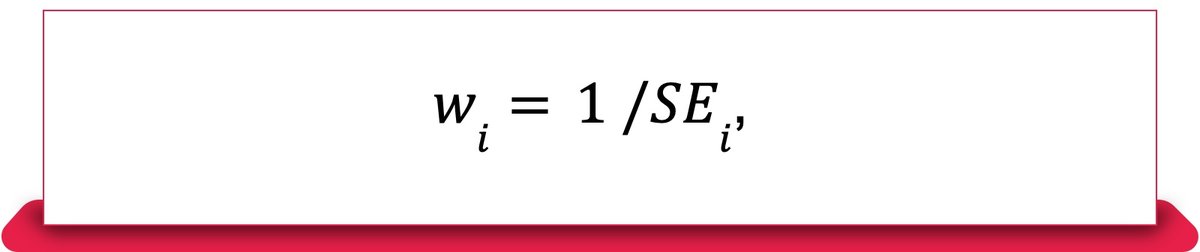Increase A/B Testing Power by Combining Experiments

Say you’ve had an experiment that produced some surprising results, so you replicated it with a new experiment. Or say you’ve got a number of separate experiments for multiple channels, yielding different reports from the same hypothesis. In the past, this would have potentially provided under-powered experiment reports without sound evidence. But there’s a more powerful way to increase our ability to measure a signal. 

At eBay, experimenters often collect several rounds of samples for the same hypothesis in an A/B test, or replicate an experiment that had surprising results. Sometimes, experimenters might also conduct separate experiments for each site or channel, which produces different reports of the same hypothesis. Say experimenters want to measure the effect of a new design to be rolled out on all eBay sites. To speed up the decision, they don’t have to wait until the new design is implemented on all 20+ eBay sites if it can not be done all at once in one sprint. Instead, they can gradually execute separate experiments site by site and demand a combined report at the end. The separate set-up is often due to engineering considerations and curious Analysts/Product Manager about the combined readout.

In this article, we discuss a powerful meta-analysis method, weighted z-test, which can combine readouts (including p-values, lift, CI, etc) from multiple independent experiments for the same hypothesis. As discussed by Dmitri Zaykin, a biostatistician at NIH, it effectively increases power and, thus, the ability to measure a signal. Many industrial practitioners often consider Fisher’s meta-analysis, as mentioned by Kohavi, an influencer in A/B testing. However, Fisher’s meta-analysis can only work for one-sided tests. In eBay, we applied the weighted z-test carefully and would like to share our practices with other early adopters.

The weighted z-test brings several benefits at zero cost. By leveraging all the collected samples in different experiments, the z-test makes the combined readout more powerful, producing the effectiveness of a much larger and more robust experiment. If you have under-powered experiments owing to factors like a small sample size, you can combine them to produce higher statistical power, smaller confidence intervals (CI) and fewer false positives. This combined p-value can be used to support a hypothesis tested in several experiments, so a series of non-significant results may now collectively suggest significance.

Weighted Z-Test 

Let’s look at some of the technical details.¹  

To understand how to combine p-values, first assume that we observe k experiments with p-value p_i and z-statistic Z_i for the i-th experiments. The weighted z-test also utilizes an experiment-specific weight, w_i, for each experiment. As discussed by Dmitri Zaykin, we use these different weights to combine independent tests to maximize the power. 

For the k experiments, the weighted z-test two-sided p-value is

where Z_i is the z-statistic of the i-th experiment.

Lipták suggested that the weights in this method “should be chosen proportional to the ‘expected’ difference between the null hypothesis and the real situation and inversely proportional to the standard deviation of the statistic used in the i-th experiment.”²

Because heterogeneity may affect the variance, we use the standard deviation of each experiment, $SE_i$, to weight each z-test statistic:

Where $SE_i = sqrt{frac{S_{iT}^2}{n_{iT}} + frac{S_{iC}^2}{n_{iC}}}$ (note that $S_{iT}$ and $S_{iC}$ are the standard deviation of i-th experiment’s treatment and control groups.)

Increasing more power

In addition, we can use a simple baseline method which pools all the samples in each experiment together and computes the z-statistic and p-value.

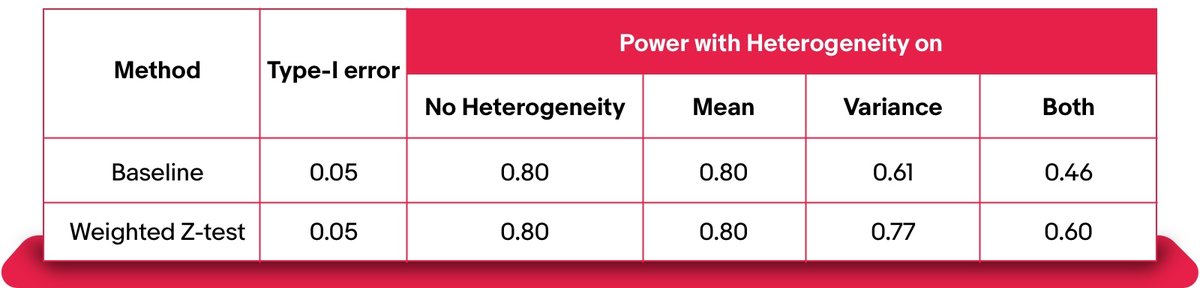
The simulations below compare the power between the baseline and weighted z-test. In particular, we consider three situations with heterogeneity effects:

1. Randomly selected mean for the two experiments, but same unit variance

2. Randomly selected variance for the two experiments, but same mean value

3. Randomly selected both mean and variance for the two experiments

 Below, you can see that the weighted z-test achieves better power without any deterioration of Type-I error, especially when there exist heterogeneity effects on variance. 

Applying in eBay

To exploit the power of the weighted z-test, these experiments we want to combine can be executed orthogonally (for example, in different planes or swim lanes) or mutually exclusively (on different sites or channels). All we needed are two assumptions, which are frequently satisfied:

1. Test the same hypothesis for all experiments (e.g., same variants)

2. Combine independent statistical tests with each other

In eBay, specifically, the two assumptions are formed into six checks:

1. The data collection of experiments must be completed

2. No quality issues that avoid best practice (e.g., more than one week, no sample delta, etc)

3. Equal traffic allocation ratio between treatment and control

4. No shared control for any two experiments

5. No more than a one week difference between the experiment durations

6. No more than a three month difference between experiment start dates

When an experimenter requests to combine several experiments, Touchstone (eBay’s experimentation platform) automatically runs the checks. After passing all six checks, the experimenter is ready to combine readouts to increase the statistical power. Below, we illustrate the procedures with an eBay example.

An eBay Example

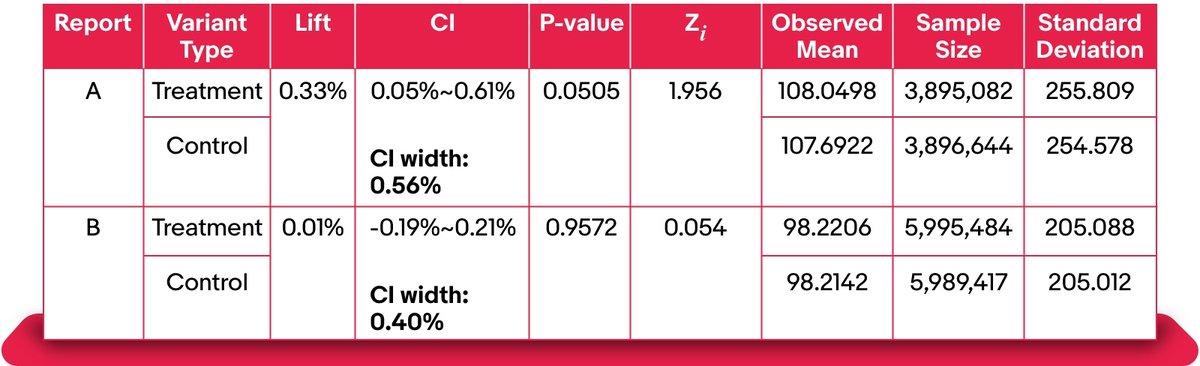
Consider the case where experimenters want to combine two reports, Experiment A and Experiment B, which both pass our assumption checks. The domain team wants to measure the impact on the shopping experience if they recommend items to users without de-duplicating based on previously viewed or clicked items, so the treatment variant is to remove the de-duplicating rules for all the placements on the View Item page. They implement the treatment for the eBay website and native app separately, so the experimenter collects samples through two different experiments (one is for the eBay website, the other is for the native app). 

Below, we provide an example of how to combine results for the metric M. 

In the each individual report, we have:

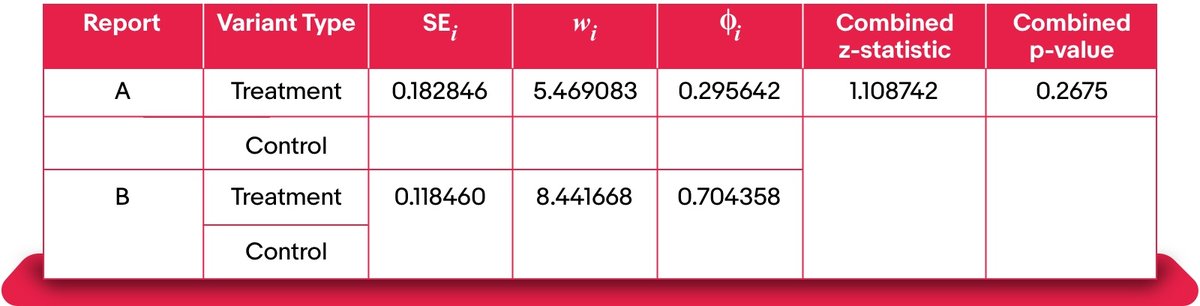
Step 1: Compute standard error per experiment using $SE_i = sqrt{frac{S_{iT}^2}{n_{iT}} + frac{S_{iC}^2}{n_{iC}}}$, where $S_{iT}$ and $S_{iC}$ are the standard deviations of i-th experiment’s treatment and control groups, respectively. 

Step 2: Compute the weights $w_i = 1mathop{/}SE_{i}$ and normalized weight $phi_i = frac{w_i^2}{sum_{i=1}^k{w_i^2}}$ that satisfy the property $sum_{i=1}^{k}{phi_i}=1$, which helps provide an interpretable combination. 

Step 3: Compute combined z-statistics: $Z_{combined}=frac{sum_{i=1}^k{w_iZ_i}}{sqrt{sum_{i=1}^k{w_i^2}}}$

Step 4: Compute combined p-value: $p_{combined}=2times[1-Phi(left|Z_{combined}right|)]$

 Step 5: compute Combined Lift, CI and means. 

1. $mu_{T} = sum_{i=1}^{k}{phi_i mu_{iT}}$ $mu_{C} = sum_{i=1}^{k}{phi_i mu_{iC}}$ $Delta_{combined} = mu_{T}  – mu_{C}$

2. $SE_{combined}=sqrt{sum_{i=1}^kphi_i^2SE_i^2}$

By combining experiments, we shrink the confidence interval, CI: the combination is more sensitive than each of the original experiments. 

Conclusion

In eBay, we leverage the weighted z-testin Touchstone (eBay’s experimentation platform) and provide experimenters an option to compute a combined test statistic when experimenters have several independent experiments with the same hypothesis. It effectively combines all the collected samples, provides more power and increases the ability to measure weak signals. The option is now available for product managers and analysts within eBay.

 

References

1. Advanced readers can check Dmitri Zaykin’s paper for a more in-depth discussion.

2. Lipták, T. (1958). On the combination of independent tests.